Machine Learning and Neural Network Terminology:
Before diving into examples on using keras with tensorFlow, it is important to go over some key terminology to understand how keras is structured and implemented as a deep learning framework. The goal of machine learning is to develop a model that can find certain patterns in a data set and learn from these patterns to make generalizations about new, previously unseen data. The label, often called the target, is what is being predicted, the intended output. Features are the input, meaning what is being used to help make predictions about data. Labeled examples contain both a set of features and their corresponding label, which is used in the training process. Once trained, the model can be used to make predictions about unlabeled examples, which is the new data.
The two most common types of machine learning models are categorical classification and regression. Categorical is when the labels are a set of categories, such as interpreting handwritten single digit numbers as a number 0-9 or matching low resolution images of fashion items as a corresponding category of clothing. Regression models predict a certain value or specified output, like the price of houses in California or the fuel efficiency of automobiles.
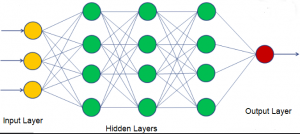
In the case of keras, the model is a neural network consisting of inputs, hidden layers, and a predicted output. Hidden layers are necessary for the model to extract important information about the data and represent the model’s ability to see patterns and connections between features and labels. Each hidden layer consists of a specified number of neurons/nodes, also called hidden units. Weights are the strength of the connections between neurons of different layers, and can be thought of as a ‘confidence’ level surrounding a certain perceived pattern.
Neural networks find patterns and make generalizations and predictions by being trained on a training data set. Since it is just as important to know how well your model can make accurate predictions on new, previously unseen data, in addition to training sets will be test sets. The test set cannot be included as part of the training set (it has to be new data), but it does has to accurately reflect the trends of the training set.
Another important part of the training process is computing loss. Loss defines how far off the predicted output is from the actual output. During training, the model makes multiple rounds of analyzing the data. Each round is known as an epoch, and this iterative process is what allows the data to learn and develop patterns. Ideally, as the model trains and the number of epochs increases, the total loss should rapidly decrease at first, then flatten out until it converges on a minimum loss. This process of training and minimizing loss is known as gradient descent optimization. The speed at which the model is able to converge on a minimum loss is known as the learning rate.
There are complications with training neural networks. One important one is the idea of overfitting, which occurs when the model is more accurate at predicting the training set than on new data its never seen before, and occurs when you train the model too much. Overfitting can be fixed using various methods, which will be discussed later in this post.
keras with TensorFlow:
The first step before creating any model on tensorFlow is to download the necessary libraries. A common library that is used is pandas, which uses the classes DataFrame and Series to break down numerical data into neat columns and rows.
from __future__ import absolute_import, division,
import matplotlib.pyplot as plt
import pandas as pd
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
print(tf.__version__)
Next, you must define your training set and data set, separating the features from the labels. The following example is from a categorical model type.
categorical_example = yourdata.categorical_example
(train_data, train_labels), (test_data, test_labels) = yourdata.load_data()
In most cases, some sort of data preprocessing is necessary before training the neural network. For example, if the data is a set of images of handwritten single digit numbers, with each pixel value in the range of 0-255, we must re-scale this to a range of 0-1. The 0-1 scale will later represent whether the pixel is totally full of writing (1) or completely vacant of writing (0), or somewhere in between. This scaling can be used by the neural networks to find patterns, helping it to identify the image as the correct single digit number.
Once the data is preprocessed, keras builds a model by creating the layers in the neural network. The most common type of model is a stack of layers, the tf.keras.Sequential model.
model = keras.Sequential([
keras.layers.Dense(16, activation=tf.nn.relu),
keras.layers.Dense(16, activation=tf.nn.relu),
keras.layers.Dense(1, activation=tf.nn.sigmoid)
])
In this example neural network model, there are 2 hidden layers and 1 output layer. The Dense stands for densely-connected, or fully-connected, neural layers. The number 16 represents the number of nodes (hidden units) in each layer. Increasing the number of nodes can increase the the capacity for the model to quickly train and find patterns, but can lead to overfitting. The last layer is densely connected with a single output node. Using the sigmoid activation function, this layer outputs a float between 0 and 1, representing a probability, or confidence level of a certain category or prediction.
Another part of building every model is having a loss function, optimizer, and metrics. The goal is to minimize the loss function, which measures how accurate the model is during training. The optimizer shows how the model is updated based on the data it sees and its loss function. Finally, the metrics monitors the training and testing sets. Accuracy is a common tool used in metrics, which measures the fraction of data that have been correctly classified or predicted.
model.compile(optimizer='insert type of optimizer here',
loss='insert loss function, often mean_squared_error',
metrics=[' insert type of metrics, often accuracy'])
Once we have built the neural network, we are ready to train it. A very basic example is shown below, with the number of epochs chosen by the user. Increasing the number of epochs can help the model train but can also lead to overfitting.
model.fit(train_data, train_labels, epochs=5)
We must also evaluate how well the model can make predictions by testing it with the testing data set.
results = model.evaluate(test_data, test_labels)
Creating visuals, such as a graph representing loss by number of epochs, can be a useful tool for analyzing the model and determining if overfitting is an issue.
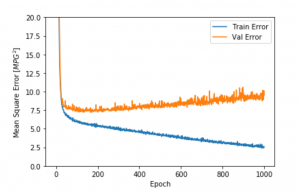
In the graph above, orange is the testing or validation set error and blue is the training error. Notice how error is significantly higher with the test data. This is an example of overfitting.
Fixing Overfitting:
There are multiple ways to fix the common issue of overfitting, in which the model is unable to accurately make predictions about new sets of data. One strategy is to decrease the number of nodes in each hidden layer. While decreasing the number of nodes restricts the computational capacity of the network, it forces the network to only find the most common patterns and make more generalizations, which fits better to new data. The following graph is an example of decreasing and increasing the number of nodes, with blue as the baseline model, green as the bigger model, and orange the smaller model. Notice that the bigger model trains much more rapidly (solid lines), but the smaller model has a much smaller error (dotted lines).
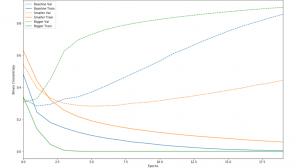
Another way to tackle overfitting is to reduce the number of epochs. Usually, overfitting will occur when there is too much training, allowing the model to find too many patterns specific to the training set. Decreasing the number of rounds of analyzing the data set (epochs) can help fix this problem. The final method is more complex. This method, known as regularization, involves restricting the quantity and type of information your model can store. Like decreasing the number of nodes, these restrictions force the model to focus only on the most common patterns and to make more generalizations.
References:
https://www.tensorflow.org/tutorials/
https://developers.google.com/machine-learning/crash-course/first-steps-with-tensorflow/programming-exercises
https://colab.research.google.com/notebooks/mlcc/intro_to_pandas.ipynb?utm_source=mlcc&utm_campaign=colab-external&utm_medium=referral&utm_content=pandas-colab&hl=en#scrollTo=WrkBjfz5kEQu
https://www.datacamp.com/community/tutorials/neural-network-models-r